Fundamentals of Large Language Models - Ep.3: Attention
Previous: Sequence-to-Sequence (Seq2Seq)
In the last post, we learned about Seq2Seq model. Regularly, we use only the last hidden state of the encoder as an input to the decoder at the very first decoding time step. However, this means that the last encoder hidden state is expected to contain all the necessary information for the decoder to do its job. Attention allows the decoder to make use all of the encoder’s hidden states. To do this, at every decoding time step, attention mechanism assigns different weighting to each of the encoder’s hidden states based on the decoder’s hidden states at the corresponding time step.
Note 1: I mentioned above that “… at every decoding time step, attention mechanism assigns different weighting to each of the encoder’s hidden states based on the decoder’s hidden states at the corresponding time step”. However, to my understanding, the weighting can also be a function of the decoder’s input at the corresponding time step. For the sake of simplicity, we will stick with using the decoder’s hidden states in the rest of this article.
Note 2: In the original paper, the authors introduced attention with bidirectional encoder architecture. However, for the sake of simplicity, we will use standard recurrent encoder architecture in this article.
Attention mechanism
If we remember from the previous article about Seq2Seq, Seq2Seq first encodes an input sequence into an embedding using an encoder network to capture all the information we need from the input sequence that allows a decoder network to generate an output sequence. More formally, an encoder \(E\) first takes an input \(x\) and produces a hidden state at the last time step \(h^E_T\). The encoder hidden state \(h^E_T\) is then passed to a decoder \(D\) (e.g., another recurrent neural network) to be decoded into an output sequence \(\hat{y}\).
Instead of using only \(h^E_T\), attention mechanism allows the decoder to use \(h^E_t \ \forall \ t \in \{1, ..., T\}\) at every decoding time step. This is done by learning a weighting function that determines how important \(h^E_t \ \forall \ t\) is at every time step. This weighting function is essentially another very small neural network, let’s call it \(A\). To learn this weighting function, at every decoding time step, we pass the decoder’s hidden state at the previous time step together with each of \(h^E_t \ \forall \ t \in \{1, ..., T\}\), which will generate \(T\) unnormalized scores. We then apply softmax to these scores to get the normalized weights, multiply each of the weights with \(h^E_t \ \forall \ t\), and sum them all up to obtain the context vector \(c_t\). To give an example, the figure below illustrates how we can compute the context \(c_1\) that we are going to use for the first decoding time step.
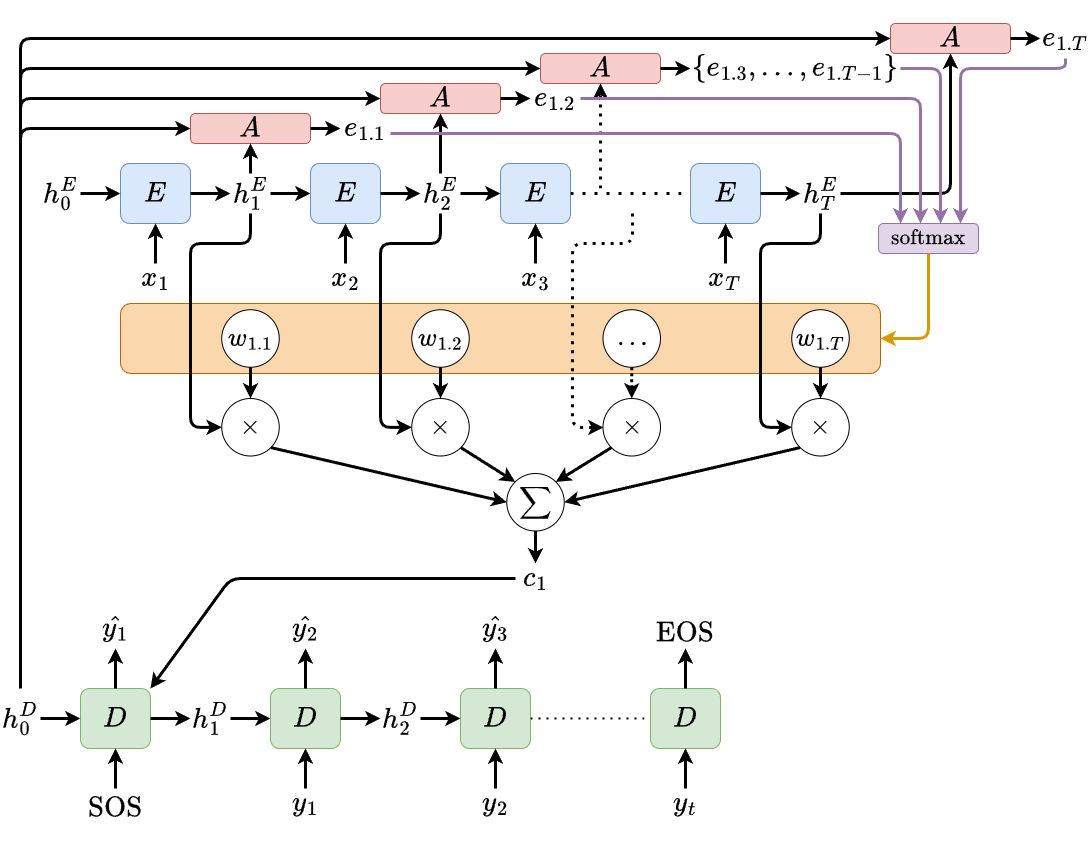
Once we obtain \(c_t\), then the rest of the training or inference processes are similar to standard Seq2Seq without attention.
Summary
We can see that attention mechanism allows the decoder to learn on which hidden states is influential or useful at every time step. This is in contrast with standard Seq2Seq architecture where we only use the last encoder’s hidden state. Please feel free to send me an email if you have questions, suggestions, or if you found some mistakes in this article.
References
Dzmitry Bahdanau, Kyunghyun Cho, Yoshua Bengio. Neural Machine Translation by Jointly Learning to Align and Translate. International Conference on Learning Representations, 2015.