Robotik - Ep.7: State Estimation with Particle Filter
Previous: State Estimation with Kalman Filter
In this post we will talk about another well known state estimation algorithm known as the particle filter. Similar to the previous post about the Kalman filter, I am not going to go over the math in detail. The goal is so that we can first build our intuition on what particle filter is doing. Let’s jump in!
Particle Filter
Robots use sensors to estimate its state. However, sensors are noisy and should not be fully trusted. Particle filter allows us to do state estimation by considering the most likely state based on our sensor measurements. This is achieved using a set of particles, where each particle \(p^i\) represents a state \(s^i\) with its associated weight \(w^i\). So for example, in the context of state estimation (e.g., localization), each particle represents how likely the robot is located at a particular state.
The algorithm is as follows. First, we initialize the particle filter by sampling \(M\) particles. Usually the initial set of particles can be sampled uniformly from the set of all possible states (i.e., uniform sampling). Given a control signal \(u_t\), we “move” all the particles (i.e., the state associated with each particle) that we currently have following the motion model of the robot. After this, we take a measurement \(z_t\) (which we can get from our sensor) and update the weights of each particle based on how likely we are to measure \(z_t\) if the robot was located at the corresponding state of each particle (e.g., \(p(z \vert s)\)). We then resample all the particles, not uniformly, but according to the weights of each particle (i.e., the ones with higher weights are more likely to be sampled). This means that the particles that have high weights will be sampled more often, while the ones with low weights may not be sampled at all. There are different options to obtain the predicted (i.e., filtered) state. In this article, we will do the simplest approach by taking the mean of the resampled particles. We then repeat this process everytime we have new \(u_t\) and \(z_t\). In practice, we may not know what \(p(z \vert s)\) is, so we may need other ways to compute the particle weight. We will see this later in the example.
The above algorithm is the basic algorithm for the particle filter. It has multiple problems associated with it and thus there are many other variations of the algorithm that address these problems. For example, the performance of above algorithm will be largely affected by the initial set of particles because during resampling step, we only sample particles from the set of initial particles. Thus, it is possible that we may not even have particles that are near the correct state. This problem is sometimes known as particle deprivation. To help alleviate this problem a little bit, during resampling step, instead of sampling completely from the set of particles that we currently have according to their weights, we can sample a small percentage of particles randomly from the set of all possible particles.
Let’s take a look at an example.
Example
Consider a robot moving in a room without obstacles. The robot is equipped with two sensors to measure distance between the robot and the walls, which allows the robot to measure the location of the robot (i.e., \(x\) and \(y\) positions) in the room. For the sake of simplicity, assume the sensors to directly return the noisy measurement of \((x,y)\) location in the room.
Say the state of the robot is its \(x\) and \(y\) position in the room, and the control inputs are the velocity in each direction \(v_x\) and \(v_y\). The robot is initialized at \((x,y) = (0,0)\), and moves by applying constant control inputs \(v_x = v_y = 0.01\). At each time step, after applying a control signal, the robot can take a measurement using the sensors to have an idea where the robot currently is.
Say we are given the two initial particles \(p^1\) and \(p^2\), where the states associated with them are \(s^1 = \begin{bmatrix} 0 \\ 0 \end{bmatrix}\) and \(s^2 = \begin{bmatrix}0.1 \\ 0.2 \end{bmatrix}\), respectively. Given the motion model:
\[s_t = s_{t-1} + u_t\]What is the state estimation after 1 time step if \(\mathbf{u}_{t=1} = \begin{bmatrix} 0.01 \\ 0.01 \end{bmatrix}\) and \(\mathbf{z}_{t=1} = \begin{bmatrix}0.012 \\ 0.009 \end{bmatrix}\) (this is the measurement the robot gets after applying the control command \(\mathbf{u}_t\))?
First, let’s move both particles by applying \(u_t\) to \(s^1\) and \(s^2\):
\[s^1_{t=1} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} + \begin{bmatrix} 0.01 \\ 0.01 \end{bmatrix} = \begin{bmatrix} 0.01 \\ 0.01 \end{bmatrix}\] \[s^2_{t=1} = \begin{bmatrix} 0.1 \\ 0.2 \end{bmatrix} + \begin{bmatrix} 0.01 \\ 0.01 \end{bmatrix} = \begin{bmatrix} 0.11 \\ 0.21 \end{bmatrix}\]We then take the measurement \(\mathbf{z}_{t=1}\) and perform the weight update step. Since we do not actually know what \(p(z \vert s)\) is, we can compute the weight of each particle based on how far it is from the measurement. Intuitively, the larger the distance between \(s\) and \(\mathbf{z}_{t=1}\) is, the lower the probability for the robot to measure \(z_t\) if the it was at state \(s\). For example, here, the distance between \(s^1\) and \(\mathbf{z}_{t=1}\) is
\[d^1 = ||s^1_{t=1} - \mathbf{z}_{t=1}||_2 = 0.00224\]We can then compute the weight \(w_1\) as the inverse of the distance:
\[w^1 = \frac{1}{d^1} = 447.2136\]Following the same procedure, we should get \(w^2 = 4.4719\). There are other ways to compute the weights but this is one simple way to do it.
Once we have the weights, we resample all the particles based on the new weights. For instance, we can compute the probability for \(p^1\) to be resampled as \(\frac{w^1}{w^1 + w^2} = 0.99\). The probability for \(p^2\) to be resampled is then 0.01.
To obtain the predicted state, one option is to use the mean of the resampled states as the predicted state. If we sampled \(p^1\) twice during resampling step, the predicted state is \(\frac{s^1_{t=1} + s^1_{t=1}}{2} = s^1_{t=1}\). This is not the only way to do it, but it is one of the simplest :)
Summary
To summarize, particle filter works as following:
-
Initialize \(M\) particles
-
Whenever we apply a control signal \(u_t\) to our robot, we also move all the particles according to our motion model
-
Get measurement \(\mathbf{z}_{t}\) and update the weights of the particles
-
Resample particles based on the new weights. Note that as discussed above, we may also sample some small percentage of the particles randomly to avoid particle deprivation, or perform other more advanced techniques.
-
Repeat from step 2.
Note that it will take some time for the particles to “converge” to the true state. This is because initially the particles were spawned randomly so it will not produce a good estimation until we have enough measurements. Here is a visualization of how the particles are evolving over time:
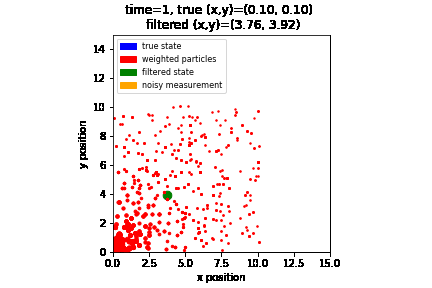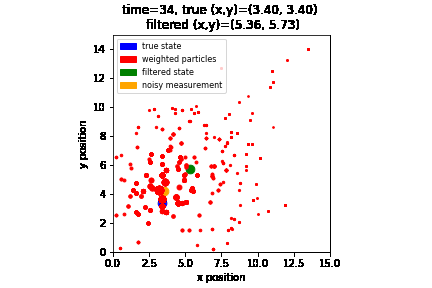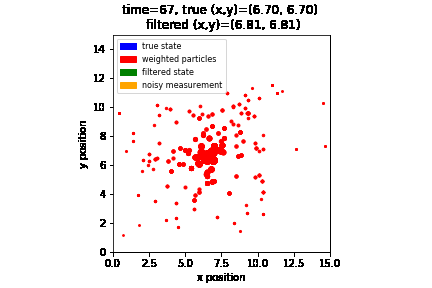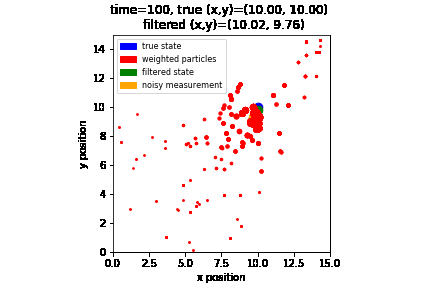
As we see, the particles (i.e., red dots) that are closer to where the robot is (i.e., blue dot) are getting bigger over time (i.e., gain more weights) as the robot moves and collect more measurements. Here, the state predicted by the particle filter is visualized as the green dot, while the sensor measurement is visualized as the orange dot.
We also only talked about one of the simplest implementation of particle filter. What can we do to improve the performance? Increasing the number of particles may improve the performance. However, while having more particles corresponds to better approximation of the true distribution that we are trying to estimate, it makes computation to be more expensive, so this can be a limitation depending on the hardware used. There are many variants that work much better than the one presented here, so I encourage you to read more about them if you are interested!
That’s it! If done properly, we can potentially have a better state estimation with particle filter compared to our noisy sensors. As always, please feel free to send me an email if you have questions, suggestions, or if you found some mistakes in this article :)
Next: TBD