Fundamentals of Large Language Models - Ep.1: Word Embeddings
In this post, we will discuss how to represent a word numerically. We refer to this numerical representation of words as word embeddings. In particular, we will take a look at learning-based approach to word embedding.
Word Embeddings
For a computer to understand, a word or a string needs to be converted into some numerical representation. But how can we represent words in a meaningful way? One naive way to represent them is by using one-hot encoded vector where the length of the vector is the same as number of words in a dictionary \(D\) that contains all of the available words. For example, the word “cup” and “mug” can be represented as
\[\small \textrm{cup} = \begin{bmatrix} 0 & 0 & 0 & \cdots & 1 & \cdots & 0 \end{bmatrix} \ \ \ \ \textrm{mug} = \begin{bmatrix} 0 & 1 & 0 & \cdots & 0 & \cdots & 0 \end{bmatrix}\]While it is a valid representation, this representation is not meaningful. For example, although the words “cup” and “mug” are semantically similar, there is no way for us to tell that that is the case from this representation. Ideally, we want their representation to be nearby in some space (i.e., \(d(x_{cup}, x_{mug})\) is small, where \(d(x_{cup}, x_{mug})\) represents the distance between the word embedding of “cup” and “mug”). Even better, the embedding would also be better if we can perform arithmetic on it, such as
\[\textrm{"king"} - \textrm{"man"} + \textrm{"woman"} = \textrm{"queen"}.\]How can one design embeddings that have these desirable properties?
Word2Vec
Word2Vec is a learning-based approach for word embedding. Word2Vec converts one-hot representation of a word into an embedding vector \(h\) with a neural network, as illustrated below.
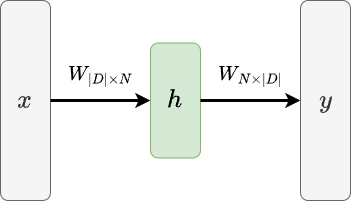
Now we might ask, what is \(y\), and how do we train this model? One variation of Word2Vec is called Continuous Bag-of-Words (CBOW) model. In CBOW, we would like our model to predict a target word in a sentence (e.g., the 3rd word in a sentence), given the context provided by the remaining words in the sentence (e.g., the 1st, 2nd, 4th, and 5th words). The following figure conceptually illustrates how CBOW model is trained.
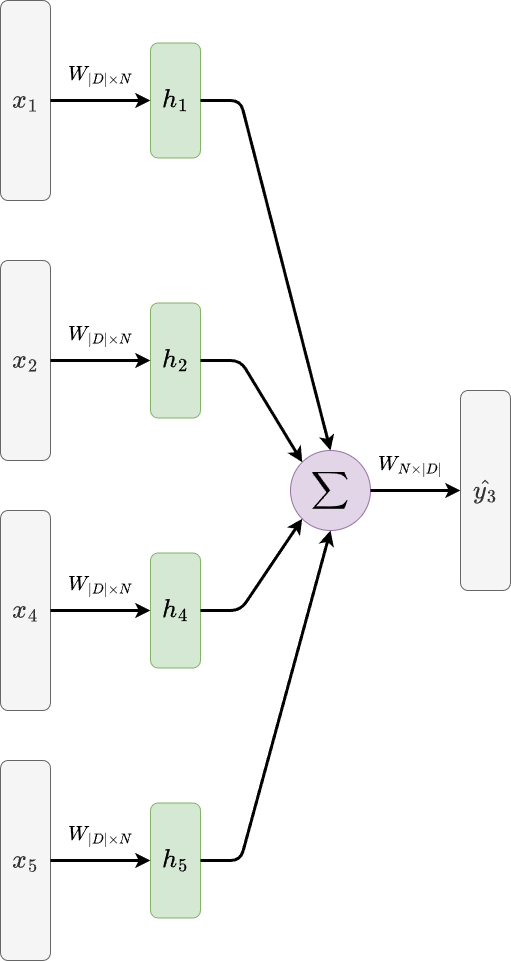
In above examples, we are given the one-hot representation of 1st, 2nd, 4th, and 5th words (i.e., \(x_1\), \(x_2\), \(x_4\), and \(x_5\)). We then project each of these one-hot representation using the first layer of our neural net, sum them all up, the project it back into categorical space with the second layer of our neural net. Since the goal in this particular example is to predict the 3rd word, we compute the categorical loss between the prediction \(\hat{y_3}\) and the one-hot representation of the 3rd word \(y_3\).
To use the trained model to embed a word, we just need to use the first layer of our neural net and project our input word one-hot representation with it.
Summary
That is it for the basics of word embeddings. There are different ways to learn word embeddings, and we might revisit this topic again in the later articles. Feel free to send me an email if you have questions, suggestions, or if you found some mistakes in this article.
References
Tomas Mikolov, Kai Chen, Greg Corrado, and Jeffrey Dean. Efficient Estimation of Word Representations in Vector Space. ArXiv, 2013.